|
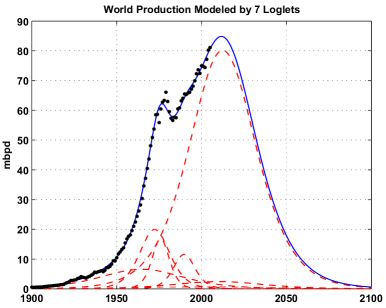
| Remember this graph? |
In reality, volumes extracted grew considerably slower than anticipated by this loglets model. Even if it captured accurately the dynamics of the petroleum system, the decline it portrayed has been considerably delayed. After all this time, how have the results from the Loglet Analysis evolved? Does it portrait a different scenario with eight data points more? This is what this work sets out to answer.
Introduction
The Loglet Analysis is a modelling technique developed two decades ago at the Rockefeller University. In simple words, it decomposes a given signal (e.g. a time series) into a set of logistic functions through an iterative fitting process. With the Loglet Analysis it is possible to assess if logistic dynamics are driving the signal in study, and in consequence to characterise the individual cycles that may compose it. For the technical details of this method please consult the Loglets white paper (or re-read Samuel's original work).
The Rockefeller University also developed a useful tool to perform the Loglet Analysis, called Loglet Lab. The University stills maintains a web page dedicated to this software, from which it may be promptly downloaded. Loglets Lab imports data series from text files or spreadsheets, providing various different views on the data and the resulting models. The user must drive the iterative fitting process, in first place choosing the number of loglets (or pulses, or cycles) to employ and then repeatedly invoking the fitting routine until improvement halts.
In Loglet Labs, the three parameters defining each pulse are presented as:
- limit - the absolute maximum reached by the logistic pulse; this is the area under the famous Hubbert curve, in petroleum matters better known as "ultimate;
- midpoint - the time at which half the limit is reached, the famous "peak";
- characteristic duration - the time that goes between 10% and 90% of the limit, providing a broad idea of the length of the pulse;
This article describes the results obtained by applying the Loglet Analysis to a recent petroleum extraction dataset. It presents the models obtained with different numbers of pulses, in order to show how results evolve with the progressive introduction of further cycles to the model.
Technical note
Loglet Lab was coded in Java, and the most recent developments seem to have taken place in 2002. Notwithstanding its age, I was able to run Loglet Labs on Oracle's Java 8 (JRE 1.8) effortlessly. There is just an issue with the start up script provided for Linux, but a direct call to the Java interpreter does it. The programme seems mostly functional; I bumped into some exceptions (see ahead) but these are likely the result of problems with internal algorithms, not brewing from a mismatch with the interpreter.
The longevity of Loglet Lab is a lesson in itself. By opting for a portable platform (Java) and choosing an open source licence, its authors guaranteed that so many years on the programme is still usable and their work keeps being referenced.
Data
In his original work Samuel Foucher used the public energy database published every year by BP. Back then I too used this convenient data source, but with time I grew wary of its accuracy. For each energy source BP publishes two different data sets: one on consumption and another on extraction/production. In recent years these datasets became ever more divergent regarding petroleum, due to the non transparent inclusion of assorted sources of non-fossil oils. The datasets on renewable energy are largely incomplete, in some cases missing almost half of the world production. Therefore I no longer consider the BP database reliable enough for any sort of modelling or analysis. I will revisit this issue at a later date in a dedicated post.
Instead I now use the public database maintained by the EIA. In this database fossil liquids can be easily unbundled from agricultural products and other accounting oddities; beyond this, a monthly dataset is also available, useful for short term analysis. This dataset provides a far more precise image of the world petroleum system.
Another important difference in this re-run of the Loglet Analysis, is the unbundling of natural gas liquids (NGLs) from liquid petroleums. Unlike fossil liquids (i.e. crude and condensates), NGL extraction has grown considerably the past decades, and at exactly the same pace of gas extraction. It does follow that these resources should be analysed separately. NGL extraction should continue to grow strongly a while longer and peak in tandem with gas. The analysis of fossil gases is left for future work. In the reminder of this article the term "petroleum" refers strictly to crude plus condensates.

One Pulse
The Loglet Analysis largely fails to approximate the original signal using a single cycle. The root mean square error (RMSE) is huge and none of the distinctive features of the world petroleum extraction profile are reproduced. Especially after 1970, the model seems almost disconnected from the signal. The ultimate estimated stands just over 1.5 Tb, clearly short, regarding what has already been consumed and what is known to exist.

This failure may be striking regarding the apparent success of the popular Hubbert Linearisation method. In reality, as commonly used, this method only fits the logistic curve to the last 30 years of data, whereas the Loglet Analysis seeks the best fit for the entire signal, starting in 1860.
Two Pulses
The picture radically changes added a second pulse. The RMSE declines dramatically and the characteristic features of the original signal start to emerge, particularly the mid-1970s peak. It is precisely the 1975-1985 period, when political factors dominated petroleum extraction, that the model struggles to reproduce the original signal. The peak comes out in 2009, just under 73 Mb/d, clearly missing the latest years. However, the ultimate now comes at 2.1 Tb, a rather credible figure.

A different way of contemplating these results is with a stacked area graph. In this form it is easier to observe the role of each loglet in the overall result. The second pulse in this case is used entirely to fit in the 1970s turmoil, with a peak in 1974.

Three Pulses
The model produced with three pulses is somewhat unexpected, in great measure decomposing in two the larger pulse of the previous model, but retaining the short pulse centred in 1974. The 1975-1985 period remains problematic, but now the most recent segment of the signal is reproduced with great fidelity. The peak is poised in 2014, just shy of 76 Mb/d. The ultimate comes out at 2.2 Tb.

In the stacked graph another feature that stands out in this model is the sharp decline after the peak. The extraction rate halves in just three decades.

Four Pulses
With the addition of a fourth loglet the model returns to the form dominated by a large pulse; however, the RMSE hardly declines and the last two data points are left at bay. The peak is positioned in 2012 at 75 Mb/d, the ultimate stands at 2.1 Tb.

All the small pulses peak close to remarkable dates: 1927 (Great Depression), 1974 (OPEC embargo to the US) and 1977 (Iranian revolution). It is important to note that the smallest pulse (Great Depression) yields an ultimate under 16 Gb.

Five Pulses
This model is clearly over-fitting, employing smaller pulses to approximate the original signal in very narrow time segments. The RMSE improves marginally, falling under 1 Mb/d for the first time. The overall peak is sited at 2010, just under 75 Mb/d. Even allowing for five pulses, the model still requires only two pulses to reproduce 95% of the global ultimate; the smallest pulse accounts for only 10 Gb (0.5% of the ultimate).

The smaller pulses again peak in coincidence with remarkable dates: 1974 (the second largest) and 1931 (the fourth largest). The third pulse is centred in 1958, possibly accounting for the three glorious decades of economic growth in the OECD after the II World War.

Six Pulses
With the six pulses Loglet Labs starts regurgitating exceptions, resulting in a premature halt to the iterative process. The final fit is likely sub-optimal (RMSE again above 1 Mb/d) but is nevertheless presented for illustrative purposes. The main features of the previous models remain: a large dominant pulse, a peak by 2010 at 75 Mb/d and an ultimate of 2.0 Tb.

The OPEC embargo to the US and the Great Depression are again present in the smaller pulses, with two others centred in the mid-1950s and late 1980s. The smallest pulse is hardly visible and accounts for only 4 Gb.

With the software failing and clear symptoms of over-fitting I felt further pulses in the analysis unnecessary.
Discussion
The first result worthy of reflection is the large failure that a single pulse analysis yields. The first 150 years of the petroleum age seem apparently unrelated to a traditional logistic process. The popular Hubbert Linearisation method is usually applied only to the last three decades, thus missing the first 120 years of petroleum extraction in the world. I discussed this subject in more detail some years ago; the Loglet Analysis reinforces the idea that the Hubbert method should not be applied at face value.
However, once a second pulse is allowed, things start falling remarkably into place. The RMSE falls dramatically and visually the model follows the data at close distance. This dramatic improvement is nevertheless achieved with mere 10% of the signal on the second pulse, thus pointing to an intrinsic logistic dynamics to the petroleum extraction process. This result also contrasts with those obtained by Samuel Foucher in 2006, in which only after allowing for five pulses did the RMSE come down significantly. The unbundling of NGLs from crude is the likely cause of this improvement, pointing to the need of independent modelling for each different quality of petroleum.
As more pulses are allowed, the main structure with a large pulse centred in 2010 and an auxiliary pulse centred in 1974 remains largely intact. The only exception is the three pulse model, that seems to split the main pulse in two, one peaking in 1990 and a second in 2020. Reinforcing what is possibly the most relevant result of this study is the fact that the two largest pulses account for at least 90% of the ultimate in all models. And apart from the three pulse model, the largest pulse accounts for at least 80%. By 2013 (the last data point) the largest pulse dominates the model in all cases.

The ultimates identified by the multi-pulse analysis fall in a narrow interval between 2 Tb and 2.2 Tb. The single pulse analysis yields an ultimate of just 1.5 Tb. These values can be considered on the low side, especially when reserves of 1 Tb of heavy petroleums are presently advertised. Albeit, cost and logistic hurdles will certainly constraint the amount of these resources that will ever be extracted. It is nevertheless important to note that the Loglet Analysis can not possibly identify cycles yet to start or in its early stages.
Conclusions and Future Work
The results of this exercise are not very different from what Samuel Foucher obtained 8 years ago. The overall shape and magnitude of the models produced today are in all similar and the sought-for peak dates remain close to the original.
World petroleum extraction is most likely following a multi-cycle logistic process. After following a standard Verhulst growth path for more than 100 years, geopolitical events introduced a clear perturbation, possibly delaying the process several decades. However, these perturbations are themselves largely logistic in nature, modelled accurately with a Loglet Analysis. In essence, about 95% of the petroleum age heretofore is explained with just two logistic cycles.
Beyond political driven cycles, this exercise also shows that there is much to gain from modelling separately different qualities of petroleum. Beyond NGLs, the model should improve further with the unbundling of heavy petroleums. Modelling the NGLs and heavy petroleum cycles is left for future work. The later is particularly difficult since it is still in its early phases (and the likely culprit for the difficulty in modelling the last two data points). Any proper forecast based on the results presented here must therefore consider the existence of these other cycles, and that their trajectory might at this stage be still largely unknown. The models produced by Jean Laherrère in this domain remain a reference.
The global peak of the different models is somewhat variable in time and value and appears mostly in the past. Pinpointing a petroleum extraction peak in time is extremely difficult and possibly a futile exercise. Moreover, geopolitical events have had a visible impact in the extraction dynamics and will likely have in the future; these are however impossible to forecast. And after all, the difference between a peak in 2012 or a peak in 2016 is probably trifling to human experience.
Acknowledgement
Beyond Loget Lab, the following software was used in this work:
Annex - detailed results
| Number of pulses | ||||||
| One | Two | Three | Four | Five | Six | |
| Ultimate (Gb) | 1 560 | 1 906 | 1 312 | 1 676 | 1 675 | 1 608 |
| Peak | 1994 | 2009 | 2020 | 2013 | 2009 | 2011 |
| Characteristic (years) | 66.6 | 78.8 | 68.3 | 70.3 | 68.2 | 67.6 |
| Ultimate (Gb) | 180 | 760 | 320 | 213 | 189 | |
| Peak | 1973 | 1990 | 1976 | 1974 | 1973 | |
| Characteristic (years) | 22.1 | 70.2 | 46.2 | 21.3 | 20.3 | |
| Ultimate (Gb) | 125 | 79 | 53 | 138 | ||
| Peak | 1974 | 1974 | 1958 | 1988 | ||
| Characteristic (years) | 17.4 | 14.6 | 26.5 | 41.1 | ||
| Ultimate (Gb) | 16 | 25 | 44 | |||
| Peak | 1927 | 1930 | 1956 | |||
| Characteristic (years) | 28.4 | 33.6 | 23.4 | |||
| Ultimate (Gb) | 17 | 32 | ||||
| Peak | 1989 | 1932 | ||||
| Characteristic (years) | 1989 | 36.9 | ||||
| Ultimate (Gb) | 1.1 | |||||
| Peak | 1993 | |||||
| Characteristic (years) | 4.18 | |||||
| Aggregate Peak | 1994 | 2009 | 2014 | 2012 | 2010 | 2010 |
| Peak rate (Mb/d) | 70.6 | 73.2 | 75.7 | 75.0 | 74.5 | 74.8 |
| Ultimate (Gb) | 1 560 | 2 086 | 2 197 | 2 091 | 1 983 | 2 013 |
I'm trying to understand whether this model has any predictive value, or whether it's just a data-fitting exercise. While I have no doubts about the imminent peak in oil in the near term future, does this model truly predict it? It seems to me that you could have selected the peak date of the primary curve at some later date, and come up with a very different result. Or do I not understand the method?
ReplyDeleteHi Don,
DeleteNo model can predict a peak date. There is just too much noise in the signal (i.e. above ground factors impacting the system) to pinpoint a year for maximum extraction. In this exercise it is patent how the peak sways around for relatively similar ultimates.
Since it is clear that petroleum extraction is essentially a logistic process, this type of model has an obvious predictive value. If the peak date is what you are interested on, a confidence interval analysis is possibly the best way to go.
Regards.
Hi Luis,
ReplyDeleteIt is by no means clear that oil extraction is a logistic process. You might try estimating Extra Heavy oil output and deducting this from EIA C+C data and re do the analysis. Jean Laherrere's estimate of C+C URR is 2700 Gb (including 500 Gb of extra heavy oil.) In my opinion he underestimates potential reserve growth. The USGS estimate of C+C less extra heavy is 3000 Gb, my expectation is about 2600 Gb without extra heavy oil and 3100 Gb for all C+C, when NGL is included the ultimate grows to about 3500 Gb (C+C+NGL). The peak will depend on extraction rates, which depends on many factors, but mostly oil prices and the state of the World Economy.
Hi DC, thanks for stopping by.
DeleteThe petroleum extraction system is a classical example of a logistic process. Petroleum is itself used to build the capital that allows for further expansion. As EROEI declines the expansion eventually folds into a decline. IMHO, Jay Forrester and is followers showed the innards of this process quite well.
Was it not a logistic process, the results of the Loglet Analysis would be different. RMSE would decline steadily with the increase of pulses and the magnitude of additional pulses would not decline.
The advantage of the Shock Model over something like the Loglet Analysis is its applicability early on, provided a discernible discovery signal. For instance, the Loglet Analysis applied at this stage to heavy petroleum will likely produce poor results. However, the extraction curve you obtained is itself very logistic-like, resembling the first derivative of the Gompertz curve, a variation of the Verhulst curve.
I believe this will get clearer with some examples where the Loglet Analysis fails. Something to explore in the future.
I am also looking forward to your take on reserve growth.
Regards.