“Net Energy and Time” is the title of an article by Nate Hagens and Hannes Kunz that attempts to assess how the lifetime of an energy system impacts its EROEI (a digest of this article was published by TheOilDrum). The main objective was to include stochastic risk in EROEI analysis – random or otherwise unpredictable events that may affect the expected output of an energy system. Considering a series of risks of this kind, Nate and Hannes slashed future energy returns, in a way proportional to the system expected lifetime. In parallel, future energy inputs were too reduced as a function of lifetime. The results of this analysis where markedly favourable to Fossil Fuels and especially negative for those systems that require most of the capital investment upfront, as is the case of many Renewable Energies.
This is a review of the “Net Energy and Time” article, pointing the factors that lead to such conclusions.
Introduction
It seems obvious, the longer an energy system has to survive to reach the energy break-even – the moment in time when total energy produced equals total energy spent on the system – the higher the risk of it failing to reach such threshold due to unpredictable or random events. If it fails to get to this milestone the system becomes a liability. But how can this reality be reflected in EROEI or net energy calculations?
To answer this question the “Net Energy and Time” article took a path that many times mangled the investor's perspective with Society's overall energy gain. The concepts of energy system and investment project are used interchangeably to produce particular inferences. Implicitly, monetary returns are mashed with energy returns leading to conclusions that, while valid financially, may not be so in a purely biophysical scope. Though presenting both perspectives in parallel, the separation is spurious, with some concerns passing from the investor to Society. The main objective of this post is to clearly set apart both perspectives, Investor versus Society, re-assessing stochastic risk from a strict biophysical stance.
Secondly, it proposes a more consistent process to calculate system lifetime impact on EROEI, as opposed to the subjective decline rates used by Nate and Hannes, for which no thorough mathematical reasoning was presented.
Offloading risk from Individual to Society
The article goes at good length explaining why returns that extend further into the future impact negatively the investor's perception of the investment's utility. Beyond net return, timing is a decisive factor, a consequence of Man's biology itself. There is good reason for that, this is the way the individual deals with events (s)he can't predict, which may prevent or alter an outcome envisioned today; an unconscious application of probability theory makes an earlier return look more attractive.
But Man is not a lonely animal, it is a sociable being by excellence. Nate and Hannes take a philosophical approach whereby Society is a bare sum of its individuals. Contrary to that, Generative Social Science has long shown that even Societies composed by the simplest of individuals can yield complex and unexpected behaviours. The latter is the stance this text adheres to, as opposed to Nate and Hannes' bare Society.
The point here is that, to Society, risks come in an entirely different manner, for a kWh is exactly the same amount of energy today or in 20 years time; the difference is that while individuals may perish in the meantime, Society prevails. Societies can perish too, but decisions taken at this level always assume such does not happen, otherwise any sort of Policy or investment decision would be irrelevant or even impossible. In this philosophical plane Policies are programmes to guarantee Society prevalence and progress.
Fortunately, mechanisms exist to offload investment risk from the individual to Society. The idea is basically to anticipate financial returns to the early years of project operation, while Society gets free or cheaper energy production during the later years of the project. Today this is accomplished with feed-in-tariffs: not only these schemes guarantee that investors get their returns independently of factors like weather variability, it also fixates financial returns and investment break-even in time. For technologies like Solar Photovoltaics (PV), some countries go further by using schemes whereby the feed-in tariff progressively diminishes with time, anticipating financial break-even to a reduced number of years. With this scheme, energy break-even remains unchanged in time, but financially the investment becomes considerably more attractive.
Feed-in tariffs or similar schemes are not referred in Nate and Hannes' article, but considering this offloading mechanism substantially changes the relevance of the risks analysed.
Looking at risks one by one
The “Net Energy And Time” analysis takes into consideration a series of potencial risks that are unpredictable when the investment project is elaborated. The risks enumerated seem all to be relevant to an individual investor, but for Society do they have the same importance? Following, each of these risks is analysed from the collective perspective.
1. Entropy
The claim here is that matter deteriorates with time, while this sentence is discussable as stated, it reports to the reality that manufactured components and parts worn out during operation. Everyone that owns a watch, a bicycle or a car is well aware of such reality, regular visits to a mechanic are mandatory to keep the machine in perfect order. It is for this reason that maintenance costs are taken into account when an energy project is assessed, either financially or energetically speaking. A proper investment project has to consider these costs, which are also used to compute the EROEI figures found in the literature. It may be claimed that longer lived energy investments require more maintenance during their productive lifetime, but then again, it is the final EROEI that matters.
While indeed material degradation adversely impacts an energy system's EROEI it can be calculated à priori, thus it doesn't represent a stochastic risk of the kind Nate and Hannes' article attempts to asses.
2. Risk of non-survival
This risk is described in a rather subjective fashion, but it is taken here as the risk an investor takes when investing on long-life technology such as Solar PV: returns may be so far ahead in time that (s)he may not live long enough to enjoy them. This is the paramount case where a feed-in tariff offloads risk from investor to Society. Survival is a clear example of a concern that applies solely to individual living things, as the investor; to the system it belongs to (e.g. Society) the survival of a particular individual is irrelevant. Thus this sort of risk shouldn't be included in whatever EROEI calculation.
3. Risk of limited access or Government Expropriation
It is impossible to justify this as a stochastic risk, for something like a wind turbine produces exactly the same energy either owned by an individual or by a state. No physical reasoning can lead to such sort of event impacting EROEI. This is perhaps the best example of the weak separation between individual and Society preconized by Nate and Hannes, a consequence of their philosophical approach to the subject.
4. Risk of Obsolescence
Apparently, the inclusion of such risk is a sharp option. An investor buying today an array of solar PV panels with a lifetime over 30 years may eventually see returns slashed if in the meantime nuclear fusion reaches maturity, sending energy prices to zero (or thereabouts). First of all this is another risk easily dealt with a feed-in tariff scheme, but beyond that, a deeper reflection should be made on what “energy obsolescence” really means. An investor may loose financial returns if nuclear fusion comes about, but if energy costs go to zero, or are greatly reduced, then the investor has a gain in everything else (s)he does. Overall, biophysical wealth increases with energy abundance, cheap energy makes everything else cheaper, for it is embodied in the production of all goods and services. This aspect is a major defining characteristic of any energy investment, setting it apart from any other asset.
If for an individual energy obsolescence may be remotely considered a risk, for Society it is not a risk at all, by the contrary, it is a gain, a “counter-risk”.
5. Risk of Destruction
This is the risk that effectively matters. For instance, a wind turbine is subject to the unpredictable effects of a tornado that may tear it apart; a solar PV array may be damaged by an heavy blizzard and so on. The longer the lifetime of an energy system the higher the risk of destruction by natural hazards. Individual or collective investors can hedge against this sort of events by insuring their investment, incurring in a monetary surplus reduction, but guaranteeing a minimum return in case of damage or destruction. Nonetheless, the total energy provided by the system will always be slashed. These risks matter because they can't be eliminated through offloading schemes to Society, an earthquake that damages an energy system always reduces its energy surplus.
Ahead it'll be introduced a proper method to recalculate EROEI taking this sort of risk into account.
Decline Rates on Energy
This is one of the key concepts of the “Net Energy and Time” article. Decline rates are used to compute the declining value of an investment against another valuable thing; in the case of money, they can be used to assess the currency's future value against physical goods. Modern paper-currencies are issued so their amount grows faster than the amount of physical goods and services created by the economy; monetary decline rates are calculated as Price Inflation rates and applied in the calculation of the future value of a currency unit. They are also used to apply interest on lending.
The first issue concerning discount rates is the figures used in the article. Arbitrary figures are chosen, starting at 5%. Why not 0.5%? or 50%? Implicitly, this figure is inferred from present interest rates applied to money. First of all it must be noted that in 2008, when inter-bank lending interest rates, such as Euribor, hit 5%, most folk seemed not to be able to afford their homes. Today it is difficult to find a bank providing interest over 4% on long term deposits to common folk.
But is money the correct entity to value energy against? When applying discount rates to energy, it must be asked against what, energy, an objective physical entity, is supposed to devalue. While the declining energy returns reflect the uncertainty of those returns coming to be, what is supposed to produce declining inputs to an energy system? Against what is the value of a future energy input declining?
The value of energy is its relative availability to Society. Energy is the more valuable to Society the scarcer it is and the less valuable the more abundant it is. This leads to asking why in the “Net Energy and Time” article are used the same discount rates for energy inputs and outputs. It is a paradox, while the amount of energy available declines per the risks considered, inputs become more affordable at the same time. This can't possibly happen and is one of the main problems with the article. If the surplus of energy is declining with time, then future inputs become more expensive, not cheaper, when compared with the relative value of other things in the Economy. If the same decline rate is to be applied to inputs and outputs of a certain project, it must be so with opposite signals: if outputs are declining in value 5 %/a, inputs must increase 5%/annum (or decrease -5 %/a).
This paradox can also be shown in another way. The "Net Energy and Time" article implies that for energy systems with high energy input later in their lifetime, EROEI increases when risk is considered. This hypothesis can be tested mathematically.
EROEI can be posed as the reason between the energy produced by a certain system and the energy spent on it. Nate and Hannes use a very simply (and wise) model for this: there's the energy spent during system startup (s), then there's an yearly energy output (o) and an yearly input for fuel, maintenance, etc (i). For a system with a lifetime of n years, EROEI can thus be presented as:
EROEI = [ o . n ] / [ s + i . n ]
Now suppose that this system is affected by some impredicted event that forces it to cease operations a number of years (m) before it's projected lifetime. Thus the new EROEI can be recalculated as:
EROEIr = [ o . (n-m) ] / [ s + i . (n-m) ]
With these expressions, the assertion that EROEI increases with risk can be presented as:
EROEI < EROEIr <=>
[ o . n ] / [ s + i . n ] < [ o . (n-m) ] / [ s + i . (n-m) ] <=>
o / [ (s / n) + i ] < o / [ [ s / (n-m) ] + i ]
which for positive o is also equivalent to:
(s / n) + i > [ s / (n-m) ] + i <=>
(s / n) > [ s / (n-m) ]
which is false when s >= 0, n >= 0, m >= 0 and n > m.
Thus the conclusion that energy systems that postpone inputs later into their operational lifetime have higher EROEI is essentially wrong. Real life works exactly in the opposite way: comparing Wind and Natural Gas systems in Europe is perhaps the best example; while for Wind, costs are fixed and known beforehand for the entire project lifetime, for Gas not only future costs are unknown, it is even questionable if enough fuel will be available later on. This issue can be put in a different perspective, by noting that Nate and Hannes do not address a very important risk: that of fuel unavailability. Either way, the options taken in the “Net Energy and Time” article in regard to future energy inputs can't possibly be justified on physical or mathematical grounds.
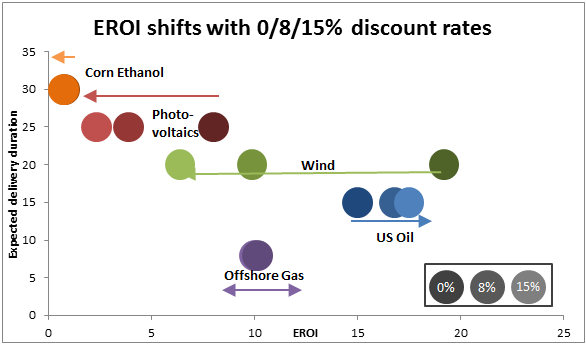
|
| The "Net Energy and Time" article is illustrated by bubble and arrows graphs like this one. All rightward arrows are wrong, arrows for renewable energies are grossly exaggerated. |
Re-Assessing EROEI in face of Stochastic Risk
As explained above, of all the risks considered, Destruction is the only one with a stochastic nature that can effectively impact the EROEI of an energy system. Assessing this risk can be made using probability theory. Assume a certain energy system may be subject to a series of natural disasters: earthquakes, tornadoes, lightening, etc. During the course of an year there's a statistical probability of each of these hazards impacting the system, call them de, dt, dl, etc. Thus a total destruction probability, dT can be computed for the system in a single year, assuming all the possible hazards are independent events:
dT = de + dt + dl + …
From probability theory it is known that the probability of an event following another is given by the product of their individual probabilities. Thus it can be determined the probability of the system lasting a certain number of years, (Pl), it is the probability of it lasting a single year raised to the number of years (n):
Pl = (1-dT)n
And thus a new time-dependent EROEI can be computed taking into account these risks:
EROEIt = EROEI . Pl
Basically, what these equations mean is that the longer an energy system is supposed to last, the more likely it is for it to be impacted by a destructive hazard. This is one of the general ideas put forward by Nate and Hannes that is entirely correct, but that unfortunately was not properly quantified. Taking as an example earthquakes hitting mainland Europe, strong enough to cause structural damage to buildings, the probability is in the order of once in every 300 years, or about 0.3% in a single year; the contrast with the 5% decline rates postulated in the article is considerable.
Several caveats must be referenced on this method. First of all, individual probabilities for each hazard or destruction risk may not be known; some risks may not even be known themselves. Second, the result of some of these hazards may not be total destruction, it may be partial destruction or temporary disability. In such cases the calculations can be refined to some extent, but the real impact of these events is largely unknown beforehand. These calculations can easily overestimate or underestimate destruction risk and their use in recalculating EROEI must be subject to a proper dose of good sense. But especially for heavy hazards, like earthquakes, they ought to be indispensable for any serious energy project.
Conclusions
The Society perspective for Net Energy or EROEI calculation is the only that has proper biophysical meaning, in the sense that it is the only one that properly accounts for the total energy flows into and out of an energy system. This perspective puts the risks considered originally by Nate and Hannes into a completely different scope, simply eliminating most of them. It also brings up other risks that were not considered, and that can significantly impact the EROEI of fossil fuels.
The employment of high declines rates to produce the increase in fossil fuel EROEI and the decline in renewables energy EROEI is a paradox, implying that energy becomes both more “expensive” and more “cheap” with time. “Expensive” and “cheap” not in paper currency terms, but in their relative abundance to Society.
While the original arrows and bubbles graphs are essentially wrong from a Society and biophysical perspective, the main postulate that long lifetime curtails the final EROEI of an energy system is entirely valid. Using probability theory it is possible to compute a somewhat objective figure enclosing the reduction of EROEI imposed by potential risks of destruction as a function of time. The objectiveness of this computation is itself a function of how well destruction risks are known.
Is a BTU today worth more or less than a BTU ten years from now?
The answer to this question is not philosophical and depends solely on the relative abundance of energy at both epochs.
No comments:
Post a Comment